P1 Lists and search
Lesson for developing algorithms in Python
Lists + Binary Search
List Operations
- aList[i] - This access your list at index i. An index is a numeric value that represents the position of an element within that data structure. For example, the first element of aList is at index 1, represented by aList[1].
- x <- aList[i] - Assigns value of aList[i] to variable x
- aList[i] <- x - Assigns value of x to aList[i]
-
aList[i] <- aList[j] - Assigns value of aList[j] to aList[i]
- INSERT(aList, i , value) - aList is the list in which you want to insert the value. i is the index at which you want to insert the value. value is the value you want to insert at that index
- APPEND(aList, value) - The value you put in is placed at the end of aList
- REMOVE(aList, i) - aList is the list in which you want to delete the value. i is the index at which you want to delete the value.
-
LENGTH(aList) - Gives you the number of elements in aList
- FOR EACH item IN aList { blah blah blah } - Item is a var assigned each element of aList in order from first element to last. The code inside the for loop is run once for every assignment of item.
1.
FOR EACH item IN aList {
PRINT(item)
}
This code iterates through each element (item) in the list aList and for each item, it prints the value of that item.
2.
FOR i FROM 0 TO LENGTH(aList) {
IF aList[i] == 42 THEN
PRINT("Found 42 at index " + i)
}
This code iterates through each index from 0 to LENGTH(aList). For each index i, it checks if the value at that index in aList is equal to 42.
If it finds 42 at any index, it prints a message indicating that it found 42 at that index.
- What does this code output

unusual, bold, away; index = 3
Comparing Python and College Board Pseudo Code
Creating a List
Python: my_list = [1, 2, 3]
Pseudo Code: my_list ← [1, 2, 3]
Accessing Elements
Python: value = my_list[index]
Pseudo Code: value <- my_list[index]
Appending Elements
Python: my_list.append(new_value)
Pseudo Code: Append new_value to my_list
Inserting Elements
Python: my_list.insert(index, new_value)
Pseudo Code: Insert new_value at index in my_list
Removing Elements
Python: my_list.remove(value)
Pseudo Code: Remove value from my_list
Modifying Elements
Python: my_list[index] = new_value
Pseudo Code: my_list[index] <- new_value
Checking Length
Python: length = len(my_list)
Pseudo Code: length <- Length of my_list
Iterating through a List
Python: for item in my_list:
{ <block of statement> }
Pseudo Code: For each item in my_list:
{ <block of statement> }
Checking for Existence
Python: if value in my_list:
{ <block of statement> }
Pseudo Code: If value is in my_list:
{ <block of statement> }
List Slicing
Python: sub_list = my_list[start:end]
Pseudo Code: sub_list <- my_list[start:end]
Popcorn Hack
Add 5 to the list in between 4 and 6 in both python and pseudo code list = [1, 2, 3, 4, 6, 7]
More Pseudo Code and Python
Psuedocode for Sum of Even Number List
Set sum to 0
For each score in the list nums:
If (score MOD 2 = 0):
Add score to sum
Display the value of sum as the sum of even numbers in the list
In Python:
nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
even_sum = 0
for score in nums:
if score % 2 == 0: # Check if the remainder when divided by 2 is 0 (even number)
even_sum += score # If previous requirement is fulfilled, add to sum
print("Sum of even numbers in the list:", even_sum)
Minimum Value List:
def find_minimum_value(input_list):
if len(input_list) == 0:
return None
min_value = input_list[0]
for num in input_list[1:]:
if num < min_value:
min_value = num
return min_value
my_list = [5, 2, 9, 1, 8, 3]
min_value = find_minimum_value(my_list)
print("Minimum value:", min_value)
Binary Search
- Binary Search is a method of searching for an element in a list.
- Binary Search is faster than Linear Search
-
How does Binary Search work?
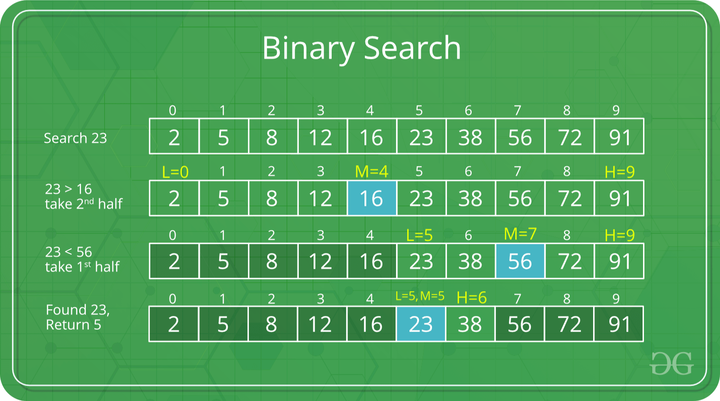
- Worst Case Scenario: 4 Iterations
arr = [2, 7, 12, 29, 33, 50, 59, 61, 68, 88, 91]
iterations = 0
def binary_search(arr, target, iterations):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
iterations += 1
if arr[mid] == target:
return mid # Element found, return its index
elif arr[mid] < target:
left = mid + 1 # Search the right half
else:
right = mid - 1 # Search the left half
target = 7
position = binary_search(arr, target, iterations)
print(f"The element {target} is at index {position}.")
print(f"Iterations: {iterations}")
Big O Notation
- Big O notation is a way to measure the upper limit of a function’s runtime.
- Common Big O Notations:
- O(1): Constant time (Ex. searching up an element by index)
- O(log n): As input size increases, time grows slowly (Binary Search!)
- O(n): Linear time: As input size increases, time grows proportionally. (Linear Search)
- O(2^n): Exponential time: Highly inefficient, as input size increases, time grows exponentially. (Brute force)
- O(n!): Factorial time: Extremely inefficient, often used to find all possible permutations of a problem.
Homework
1) Write an expression that uses list indexing and list procedures. Write comments on your code to show what each line is doing. 2) Write a python function that can determine the worst case number of iterations of a binary search for an array of length 20.
3) You have a list `myList` containing the following elements: [10, 20, 30, 40, 50].
FOR i FROM 0 TO LENGTH(myList) {
x <- myList[i]
myList[i] <- x * 2
}
What will be the final content of `myList` after executing this algorithm?
A) [20, 40, 60, 80, 100]
B) [10, 20, 30, 40, 50]
C) [10, 40, 30, 20, 50]
D) [50, 40, 30, 20, 10]